Class 12th Chemistry Chapter 3 रासायनिक बलगतिकी part 2 रासायनिक बलगतिकी का ही एक अहम् भाग है | अगर आप इस इकाई अथवा पाठ को अच्छे से अध्ययन करना चाहते है तो हम आपसे यही अनुरोध करते है कि आप इस बहुत बड़ी इकाई को छोटे छोटे part में पढ़े | यही वजह है कि हम आपको यहाँ पर part वाइज नोट्स Provide कर रहे है | इस part में जो भी महत्वपूर्ण हैडिंग है उन्हें जरूर याद करे | क्यूंकि ये ही आपको अच्छे मार्क्स प्राप्त करने में मदद करेंगी |
Table of Contents
ToggleIf you need online tutor or help for any questions like mathematics, physics, chemistry numerical or theory then you can contact me on WhatsApp on +918755084148 or click here. Our team help you all time with cheap and best price. If need it on video our team provide you short video for your problem. So keep in touch of our team specialists.
Class 12th Chemistry Chapter 3 रासायनिक बलगतिकी part 2
इस भाग में हम बोर्ड में पूछे गये कम से कम 3 से 5 मार्क्स का अध्ययन करेंगे | अत: आप इन्हें ध्यान से पढ़े | अगर आप कुछ समस्या महसूस करते है तो आप हमे सम्पर्क कर सकते हो और आप Ask Question पर क्लिक करके प्रश्न भी पूछ सतके हो | हम आपसे ये गुजारिश करते है कि आप इन महत्वपूर्ण हैडिंग को अवस्य याद करेंगे | क्यूंकि ये वो सभी हैडिंग है जो पिछले बहुत सालो के पेपर में रिपीट हुई है | अगर आप इन्हें याद करके एग्जाम में बैठते है तो आप 90 % से अधिक अंक हासिल कर सकते है |
Class 12th Chemistry Chapter 3 रासायनिक बलगतिकी part 2 में महत्वपूर्ण Headings निम्नलिखित है | इन्हें अच्छे से याद करे | ये आपको अच्छे अंक दिलाने में मदद करेगी:
- वेग नियम और उसकी व्यूत्पत्ति
- वेग स्थिरांक के अभिलाक्षणिक गुण
- अभिक्रिया के वेग और वेग स्थिरांक में अंतर
- अभिक्रिया की आण्विकता
- जटिल अभिक्रिया और अभिक्रिया की कोटि
- अभिक्रिया की आण्विकता और कोटि में अंतर
- समाकलित वेग समीकरण और शून्य कोटि की अभिक्रिया

क्या जरूर्री है क्या नही :-अच्छे से अच्छे अंक लाने के लिए आपको बेहतर नोट्स एंड बेहतर क्लास लेनी चाहिये जो आपको बिलकुल फ्री में हम यहाँ पर दे रहे है |
अत: अच्छे से हमारी वेबसाइट https://excellentshiksha.com/ से पढे हम आशा करते है की आप बेहतर अंक प्राप्त करेंगे |
वेग नियम और उसकी व्यूत्पत्ति
वेग नियम :- इस नियम के अनुसार किसी अभिक्रिया का वेग उसके अभिकारको के मोलर संद्र्ण के समानुपाती होता है |
अर्थात –


वेग स्थिरांक के अभिलाक्षणिक गुण
वेग स्थिरांक के अभिलाक्षणिक गुण :- अभिक्रिया का वेग स्थिरांक निम्नलिखित गुण प्रदर्शित करता है –
1- किसी भी अभिक्रिया का वेग उसके वेग स्थिरांक पर निर्भर करता है और यह एक दुसरे के समानुपाती होते है |
2- निश्चित तापमान पर अभिक्रिया का वेग स्थिरांक नियत रहता है |
3- वेग स्थिरांक का मान उन अभिकारको की सांद्रता पर निर्भर करता है| जिनका मान परिवर्तित होता रहता है |
अभिक्रिया के वेग और वेग स्थिरांक में अंतर
अभिक्रिया के वेग और वेग स्थिरांक में अंतर :- इनमे निम्न अंतर होता है –
| क्र0 सं0 | अभिक्रिया का वेग | वेग स्थिरांक |
|---|---|---|
| 1 | अभिक्रिया का वेग प्राय: इकाई समय में अभिकारक पदार्थो के सान्द्र्ण में परिवर्तन की दर होती है | | किसी अभिक्रिया में अभिकारको का सान्द्र्ण इकाई में होने पर उसका वेग वेग स्थिरांक कहलाता है| |
| 2 | अभिक्रिया के वेग का मान ताप पर निर्भर करता है| यह ताप वृद्धि पर बढ़ता है | | वेग स्थिरांक का मान भी ताप पर निर्भर करता है | यह भी ताप वृद्धि पर बढ़ता है| |
| 3 | अभिक्रिया के वेग का मात्रक प्राय: मोल प्रति लीटर प्रति सेकंड होता है| | यह अभिक्रिया की कोटि पर निर्भर करता है | |
| 4 | यह अभिक्रिया के प्रारम्भ होने पर घटता है| | यह सामान्यत: पूर्ण अभिक्रिया में स्थिर रहता है| |
अभिक्रिया की आण्विकता
अभिक्रिया की आण्विकता:- रासायनिक अभिक्रिया में भाग लेने वाले अणुओ की न्यूनतम संख्या या अभिक्रिया के लिए आवश्यक अणुओ की पूर्ण संख्या को उस अभिक्रिया की आण्विकता कहते है | ये निम्न प्रकार की होती है: –
1 – एक अणुक अभिक्रिया :– वे अभिक्रिया जिनमे अभिकारक का केवल एक अणु भाग लेता है एक अणुक अभिक्रिया कहलाती है |
जैसे :- H2O2 ——–> H2O+ 1/2 O2
PCl5 —————> PCl3 + Cl2
2- द्वि अणुक अभिक्रिया :- वे अभिक्रिया जिनमे अभिकारक के केवल दो अणु भाग लेते है द्वि अणुक अभिक्रिया कहलाती है |
जैसे :- CH3COOC2H5 + H2O ————–> CH3COOH + C2H5OH
H2+ I2 —————–> 2HI
3- त्रि अणुक अभिक्रिया :- वे अभिक्रिया जिनमे अभिकारक के केवल तीन अणु भाग लेते है त्रिअणुक अभिक्रिया कहलाती है|
जैसे :- 2CO + O2 ——————–> 2CO2
जटिल अभिक्रिया और अभिक्रिया की कोटि
जटिल अभिक्रिया :- वे अभिक्रिया जिनमे अभिकारक के अनेक अणु भाग लेते है जटिल अभिक्रिया कहलाती है | ये अभिक्रिया एक पद में नही होती है अर्थात ये अनेक पदों में घटित होती है |
जैसे :-
4HBr + O2 ————————–> 2H2O + 2Br2
ये निम्न पदों में होती है –
पद 1 :- HBr + O2 ————> HO-OBr (मन्द पद )
पद 2 :- HO-OBr +HBr ———–> 2HOBr ( तीर्व अभिक्रिया )
पद 3 :- [HOBr + HBr ——————>Br2 + H2O ]x2
अभिक्रिया की कोटि :– अभिकारक अणुओ की वह संख्या , जिनका संद्र्ण रासायनिक परिवर्तन के परिणाम स्वरूप परिवर्तित होता है अभिक्रिया की कोटि कहलाती है |
जैसे :- निम्नलिखित अभिक्रिया के लिए –
nA + mB ————-> Product (उत्पाद )
जब अभिक्रिया में A तथा B दोनों अभिकारको के संद्र्ण में परिवर्तन होता है | तब किसी भी क्षण पर अभीक्रिया का वेग निम्न प्रकार होता है :-
अभिक्रिया का वेग = k [A] ^ n [B]^m
इस समीकरण में घात का कुल योग अभिक्रिया की कोटि कहलाती है |
अर्थात कोटि = n + m होगी
अभिक्रिया की आन्विकता और कोटि में अंतर :-
| क्र0 सं0 | अभिक्रिया की कोटि | अभिक्रिया की आण्विकता |
|---|---|---|
| 1 | इसमें अभिक्रिया की क्रियाविधि के सम्पूर्ण पदों के विषय में विचार किया जाता है| | अभिक्रिया की आण्विकता में अभिक्रिया के किसी विशेष पद पर ही ध्यान देते है| |
| 2 | यह अभिक्रिया के वेग और अभिकारको की सांद्रता में सम्बन्ध बताती है| | यह अभिक्रिया के किसी एक विशिष्ट पद में भाग लेने वाले अणुओ की संख्या बताती है| |
| 3 | इसे प्रयोगों द्वारा ज्ञात किया जाता है | अत यह प्रायोगिक मान होता है| | इसे अनुमान से ही बता सकते है| यह सिद्धान्तिक मान होता है| |
| 4 | अभिक्रिया की कोटि पूर्णांक , भिन्न और ऋणात्मक हो सकती है| | अभिक्रिया की आण्विकता सदैव पूर्णांक होती है | |
समाकलित वेग समीकरण और शून्य कोटि की अभिक्रिया
समाकलित वेग समीकरण :- वे गणितीय समीकरण जो अभिक्रिया के वेग तथा अभिकारक की मोलर सांद्रता के मध्य सम्बन्ध को दर्शाती है वेग समीकरण कहलाती है | वेग समीकरण को समाकलित करके वेग स्थिरांक k तथा भिन्न भिन्न समय पर अभिकारक की सांद्रता के मध्य सम्बन्ध दर्शाने वाली समीकरण समाकलित समीकरण कहलाती है|
विभिन्न कोटि की अभिक्रियाए :- अभिक्रियाओ को निम्नलिखित कोटियो में वर्गीक्रत किया गया है –
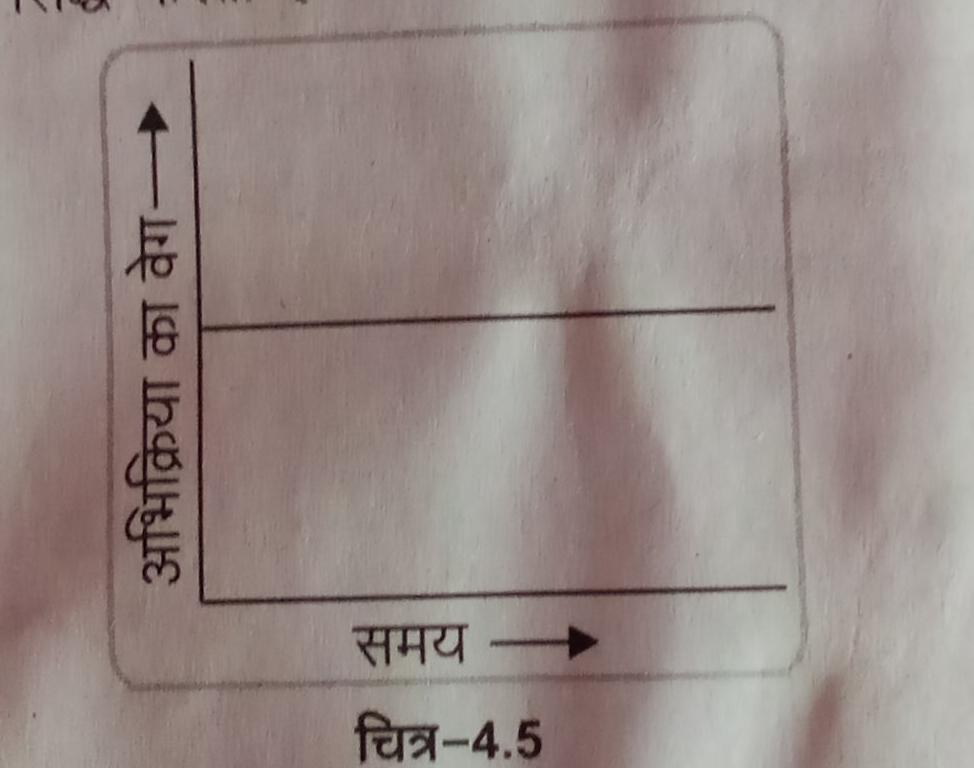
1:- शून्य कोटि की अभिक्रिया : वे अभिक्रिया जिनकी प्रगति में अभिकारक के किसी भी अणु का संद्र्ण परिवर्तित नही होता है | अर्थात जिनका वेग अभिकारक अणुओ की सांद्रता की शून्य घात के समानुपाती होता है शून्य कोटि की अभिक्रिया कहलाती है|
अर्थात –
माना की कोई शून्य कोटि की अभिक्रिया निम्न प्रकार होती है |
A ————–> B + C
माना की A की t = 0 पर प्रारम्भिक सांद्रता [A0] मोल / लीटर और t समय पर [A ] मोल / लीटर है|
तब
वेग = – d[A]/ dt = k [A]^0 = k
जहाँ k शून्य कोटि की अभिक्रिया के लिए वेग स्थिरांक है जिसका मान वेग के समान होता है|
अत: k का मात्रक मोल / लीटर / सेकंड होता है|